Robust output-feedback stabilization for incompressible flows using low-dimensional H∞-controllers

Abstract

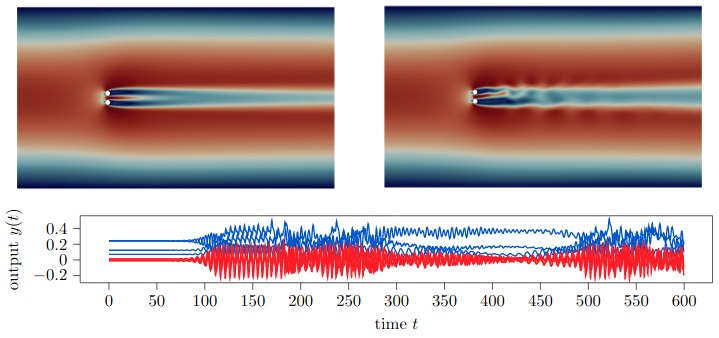
Output-based controllers are known to be fragile with respect to model uncertainties. The standard H∞-control theory provides a general approach to robust controller design based on the solution of the $$mathcal H_ınfty $$-Riccati equations. In view of stabilizing incompressible flows in simulations, two major challenges have to be addressed: the high-dimensional nature of the spatially discretized model and the differential-algebraic structure that comes with the incompressibility constraint. This work demonstrates the synthesis of low-dimensional robust controllers with guaranteed robustness margins for the stabilization of incompressible flow problems. The performance and the robustness of the reduced-order controller with respect to linearization and model reduction errors are investigated and illustrated in numerical examples.