5 Hauptkomponentenanalyse Ctd.

Im vorherigen Kapitel hatten wir einen zweidimensionalen Datensatz betrachtet und dafür die Richtung bestimmt, in der die Varianz maximal wird. Da wir außerdem ermittelt hatten, dass die Summe der Varianz unabhüngig vom Koordinatensystem ist (es muss nur ein orthogonales sein) bedeutete das gleichzeitig, dass die verbleibende Richtung die Richtung der minimalen Varianz war.

Jetzt wollen wir einen Datensatz mit mehr Merkmalen betrachten und sehen, wie die algorithmische Herangehensweise zum Verständnis beiträgt.

5.1 Der PENGUINS Datensatz

Die Grundlage ist der Pinguin Datensatz, der eine gern genommene Grundlage für die Illustration in der Datenanalyse ist. Die Daten wurden von Kristen Gorman erhoben und beinhalten 4 verschiedene Merkmale (engl. features) von einer Stichprobe von insgesamt 3443Pinguinen die 3 verschiedenen Spezies zugeordnet werden können oder sollen (Fachbegriff hier: targets). Im Beispiel werden die Klassen mit 0, 1, 2 codiert und beschreiben die Unterarten Adele, Gentoo und Chinstrap der Pinguine. Die Merkmale sind gemessene Länge und Höhe des Schnabels (hier bill), die Länge der Flosse (flipper) sowie das Köpergewicht4 (body mass).

Wir stellen uns 2-3 Fragen:

  1. Würden eventuell 3 (oder sogar nur 2) Dimensionen reichen um den Datensatz zu beschreiben?
  2. Können wir aus den Merkmalen (features) die Klasse (target) erkennen und wie machen wir gegebenenfalls die Zuordnung?

5.2 Darstellung

In höheren Dimensionen ist schon die graphische Darstellung der Daten ein Problem. Wir können aber alle möglichen 2er Kombinationen der Daten in 2D plots visualisieren.

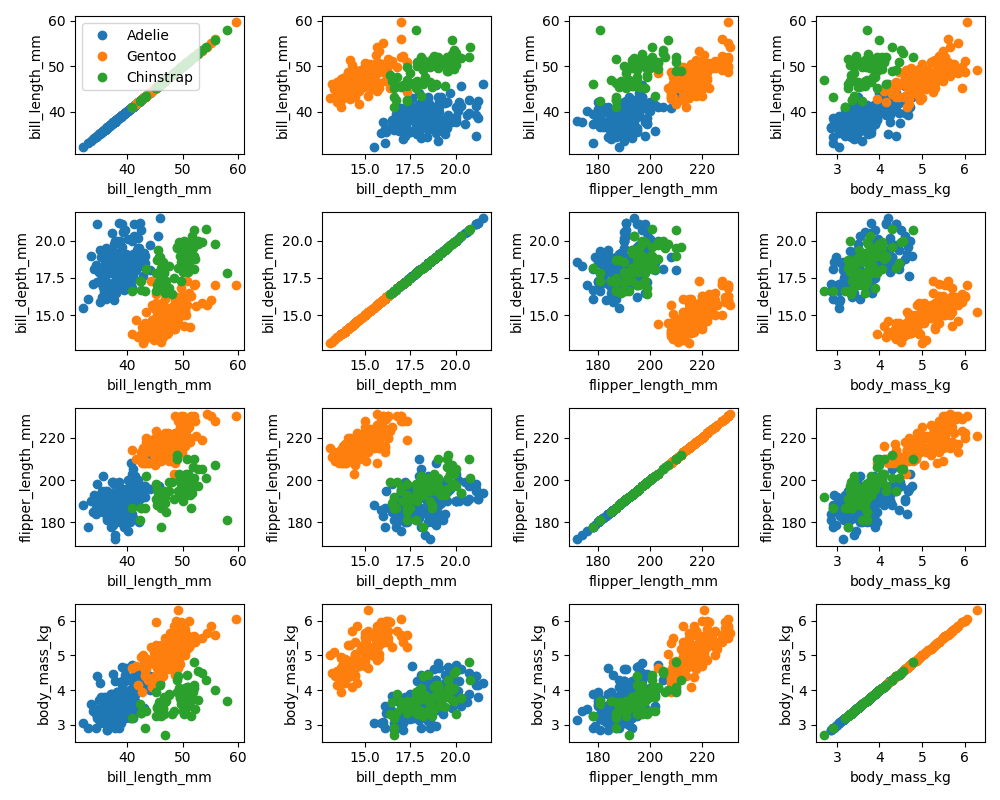
Pinguin Datenset 2D plots

Ein Blick auf die Diagonale zeigt schon, dass manche Merkmale besser geeignet als andere sind, um die Spezies zu unterscheiden, allerdings keine der Zweierkombinationen eine Eindeutige Diskriminierung erlaubt.

5.3 Korrelationen und die Kovarianzmatrix

Als nächstes suchen wir nach Korrelationen in den Daten in dem wir für alle Merkmalpaare die Korrelationen ausrechnen. Dafür berechnen wir die sogenannte Kovarianzmatrix \[\begin{equation*} \operatorname{Cov}(\mathbf X) = \begin{bmatrix} \rho_{{\mathbf{x} _ i \mathbf{x} _ j}} \end{bmatrix}_{i,j=1,\dots n} \in \mathbb R^{n\times n} \end{equation*}\] wobei \(n\) die Dimension der Daten ist und wobei \[\begin{equation*} s_{{\mathbf{x} _ i \mathbf{x} _ j}} = \frac{1}{N-1} \sum_{k=1}^N (x_{ik}-\overline{{\mathbf{x} _ i}})(x_{jk}-\overline{{\mathbf{x} _ j}} ). \end{equation*}\] die Kovarianzen sind, die wir auch schon in der ersten Vorlesung kennengelernt haben.

Ist \(\mathbf X\in \mathbb R^{N\times n}\) die Matrix mit den Datenvektoren \({\mathbf{x} _ i}\in \mathbb R^{n}\) als Spalten und ist der Datensatz zentriert so erhalten wir die Kovarianzmatrix als \[\begin{equation*} \operatorname{Cov}({\mathbf{X}}) = \frac{1}{N-1}{\mathbf{X}}^T {\mathbf{X}} \end{equation*}\]

Wir bemerken, dass auf der Hauptdiagonalen die Varianzen in Koordinatenrichtung stehen und in den Zeilen oder Spalten ein Mass dafür, wie bspw. \({\mathbf{x} _ i}\) und \({\mathbf{x} _ j}\) korreliert sind. Große Zahlen bedeuten eine große Varianz oder eine starke Korrelation und umgekehrt. Für die Datenanalyse können wir \(\operatorname{Cov}({\mathbf{X}})\) wie folgt heranziehen:

5.4 Hauptachsentransformation

Wie im vorherigen Kapitel hergeleitet, bedeutet ein Koordinatenwechsel die Multiplikation der Datenmatrix \({\mathbf{X}}\in \mathbb R^{N\times n}\) mit einer orthogonalen Matrix \(V\in \mathbb R^{n\times n}\): \[\begin{equation*} \tilde {\mathbf{X}}= {\mathbf{X}}V, \end{equation*}\] wobei \(\tilde {\mathbf{X}}\) die Daten in den neuen Koordinaten sind (die Basisvektoren sind dann die Zeilenvektoren von \(V\)). Wir wollen nun eine Basis finden, in der

  • \(\operatorname{Cov}({\mathbf{X}})\) eine Diagonalmatrix ist — damit wären alle Richtungen in den Daten unkorreliert und könnten unabhängig voneinander betrachtet werden5 –
  • und in der die neuen Varianzen nach Größe geordnet sind gleichzeitig die verfügbare Varianz maximal in wenigen Richtungen konzentrieren.

Nachden den Überlegungen im vorherigen Kapitel ist die erste Hauptrichtung durch den ersten rechten Singulärvektor \(v_1\in \mathbb R^{n}\) der (ökonomischen) Singulärwertzerlegung \[\begin{equation*} {\mathbf{X}}= U\Sigma V^* = \begin{bmatrix} u_1 & u_2 & \dots & u_n \end{bmatrix} \begin{bmatrix} \sigma_1 \\ &\sigma_2 \\ &&\ddots \\ &&&\sigma_n \end{bmatrix} \begin{bmatrix} v_1^* \\ v_2 ^* \\ \vdots \\ v_n^* \end{bmatrix} \end{equation*}\] von \(\mathbf X\in \mathbb R^{N\times n}\) gegeben. Die zugehörigen Koeffizenten berechnen wir mittels \[\begin{equation*} \tilde {\mathbf{X}}= {\mathbf{X}}v_1. \end{equation*}\]

5.5 Rekonstruktion

Um zu plausibilisieren, dass die weiteren Hauptachsen durch die weiteren (rechten) Singulärvektoren gegeben sind, betrachten wir erst die Rekonstruktion also die Darstellung im Ausgangskoordinatensystem (mit den messbaren oder interpretierbaren Features) die durch \[\begin{equation*} \tilde {\tilde {\mathbf{X}}} = {\mathbf{X}}v_1v_1^T \end{equation*}\] gegeben ist. Die letzte Formel wird vielleicht klarer, wenn Jan sich überlegt, dass für einen Datenpunkt \({\mathbf{X}}_j=\begin{bmatrix} x_{1j} &x_{2j} & \dots& x_{nj}\end{bmatrix}\) (also die \(j\)-te Zeile von \({\mathbf{X}}\)), der Koeffizient für \(v_1\) gegeben ist durch \(\alpha_j=v_1^T{\mathbf{X}}_j^T\) und die Darstellung im Vektorraum durch \[\begin{equation*} \tilde{\tilde{ {\mathbf{X}}}}_j=(\alpha_j v_1)^T = \alpha_j v_1^T = (v_1^T {\mathbf{X}}_j^T) v_1^T = {\mathbf{X}}_j v_1 v_1^T \end{equation*}\] gegeben ist.

Damit können wir mit \[\begin{equation*} {\mathbf{X}}- \tilde{\tilde {{\mathbf{X}}}} = {\mathbf{X}}(I-v_1v_1^T) \end{equation*}\] den Teil der Daten betrachten, der durch die Richtung \(v_1\) nicht abgebildet wird (sozusagen den noch verbleibenden Teil). Jan kann nachrechnen, dass wiederum \(U\) und \(V\) die Singulärvektoren von \({\mathbf{X}}-\tilde{\tilde {{\mathbf{X}}}}\) bilden, mit jetzt \(v_2\) als Richtung mit dem größten (verbleibenden) Singulärwert.

Das heißt, dass der \(k\)-te Singulärvektor die \(k\)-te Hauptrichtung bildet.

5.6 Reduktion der Daten

Ist die Datenmatrix mit linear abhängigen Spalten besetzt, äußert sich das in \(\sigma_k = 0\) für ein \(k<n\) (und alle noch folgenden Singulärwerte). Jan rechnet nach, dass dann \[\begin{equation*} {\mathbf{X}}= {\mathbf{X}}V_{k-1}V_{k-1}^T \end{equation*}\] wobei \(V_{k-1}\) die Matrix der \(k-1\) führenden Singulärvektoren ist und das entsprechende \[\begin{equation*} \tilde {\mathbf{X}}= {\mathbf{X}}V_{k-1} \end{equation*}\] alle Informationen des Datensatzes in kleinerer Dimension parametrisiert.

In der Praxis sind schon allein durch Messfehler exakte lineare Abhängigkeiten sowie durch die näherungsweise Bestimmung auf dem Computer das Auftreten von \(\sigma_k =0\) quasi ausgeschlossen. Stattdessen werden Schwellwerte definiert, unterhalb derer die SVD abgeschnitten wird.

Wie oben, werden dann die Daten \(\tilde {\mathbf{X}}={\mathbf{X}}V_{\hat k}\) in den (reduzierten) Koordinaten der Hauptachsen betrachtet sowie die Rekonstruktion \(\hat {\mathbf{X}}= {\mathbf{X}}V_{\hat k}V_{\hat k}^T\), wobei der \(V_{\hat k}\) die Matrix der \(\hat k\) führenden Singulärvektoren sind (mit Singulärwerten überhalb des Schwellwertes).

5.7 Am Beispiel der Pinguin Daten

Wir stellen die Daten noch einmal zentriert dar:

Pinguin Daten Zentriert

Figure 5.1: Pinguin Daten Zentriert

Für die Kovarianzmatrix der Pinguin Daten erhalten wir:

Covariance matrix: 
[[ 29.8071  -2.5342  50.3758   2.6056]
 [ -2.5342   3.8998 -16.213   -0.7474]
 [ 50.3758 -16.213  197.7318   9.8244]
 [  2.6056  -0.7474   9.8244   0.6431]]

Für die Singulärwerte:

In: U, S, Vh = np.linalg.svd(data, full_matrices=False)

In: print(S)
Out: [269.7858  74.1334  28.4183   7.2219]

Zwar ist hier kein Singulärwert nah an der Null, allerdings beträgt der Unterschied zwischen dem größten und dem kleinsten schon eine gute 10er Potenz, was auf eine starke Dominanz der ersten Hauptachsen hinweist.

In der Tat, plotten wir die Daten in den Koordinaten der Hauptachsen (also \(\tilde {\mathbf{X}}\)), zeigen Bilder der \(v_1\) oder \(v_2\)-Koordinaten klare Tendenzen in den Daten, während die Plots der übrigen Richtungen wie eine zufällige Punktwolke aussieht, vgl. die Abbildung hier.

Pinguin Datenset 2D plots in Hauptachsenkoordinaten

Als letztes plotten wir noch \(\hat {{\mathbf{X}}}\) für \(\hat k =2\). Das heißt wir reduzieren die Daten auf die \(v_1\) und \(v_2\)-Richtungen und betrachten die Rekonstruktion. Im Plot sehen wir, dass in gewissen Teilen die Daten gut rekonstruiert werden. Allerdings, hat \(\hat{{\mathbf{X}}}\) nur Rang \(\operatorname{Rk} \hat {{\mathbf{X}}}=2\) (warum?), sodass in den Plots notwendigerweise direkte lineare Abhängigkeiten offenbar werden.

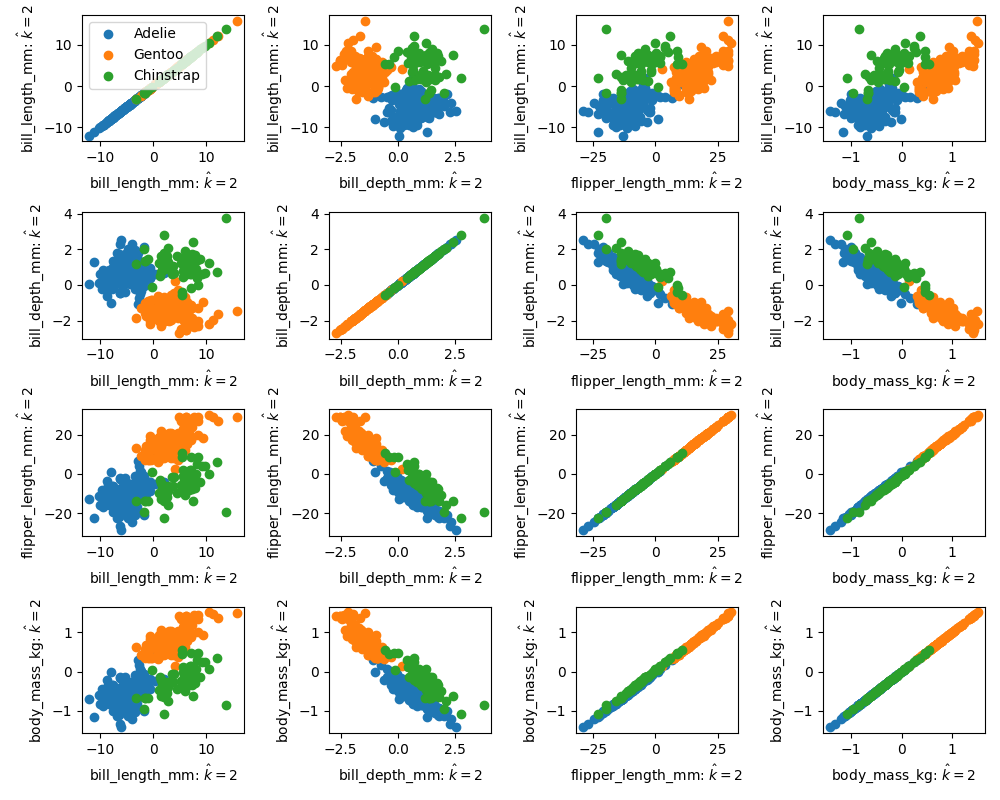
Pinguin Datenset – rekonstruiert von \(\hat k =2\) Hauptachsenkoordinaten

5.8 Aufgaben

5.8.1 Kovarianzen (P+T)

Erzeugen Sie für N aus Nl = [10, 1000, 100000] zufällige Vektoren x und y der Länge N und berechnen Sie für den Datensatz X = [x, x, x*y, y] jeweils die Matrix der Korrelationskoeffizienten \[\begin{equation*} \rho _{i\;j} = \frac{s_{i\, j}}{s_i \cdot s_j} \end{equation*}\] wobei \(s_{i\,j}\) die Kovarianz der Daten \({\mathbf{x} _ i}\) und \({\mathbf{x} _ j}\) ist und \(s_{i}\) die Varianz von \({\mathbf{x} _ i}\). Interpretieren sie die Ergebnisse.

Hinweis: Weil Zufälligkeit involviert ist, ist die Interpretation manchmal schwierig. Lassen sie das Programm öfter laufen und beobachten sie verschiedene Realisierungen der Stichproben.

import numpy as np

# N = 10

x = np.random.randn(10, 1)
y = np.random.randn(10, 1)

X = np.hstack([x, x, x*y, y])

Xcntrd = X - X.mean(axis=0)
# zentrieren der Daten

# Kovarianz Matrix ausrechnen
covX = 1/(10-1)*Xcntrd.T @ Xcntrd

# Varianzen -- stehen auf der Diagonalen im Quadrat
varvec = np.sqrt(np.diagonal(covX)).reshape(4, 1)
# Matrix mit den Kombinationen aller Varianzen
varmat = varvec @ varvec.T

matcc = covX * 1/varmat

print(f'N={10} : Matrix of Correlation Coefficients=')
print(matcc)

5.8.2 Pinguin Datensatz – Targets Plotten (P)

Laden Sie die Pinguin Datensatz (hier als json file bereitgestellt) und plotten sie bill_length versus flipper_length für die drei Spezies Adelie, Gentoo, Chinstrap in drei separaten Grafiken.

import json

import numpy as np
import matplotlib.pyplot as plt

with open('penguin-data.json', 'r') as f:
    datadict = json.load(f)

print(datadict.keys())

data = np.array(datadict['data'])
target = np.array(datadict['target'])
feature_names = datadict['feature_names']
target_names = datadict['target_names']

print('target names: ', target_names)
print('feature names: ', feature_names)

fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(10, 3))

# # Ein Vektor der aus dem Target Vektor das target 0 raussucht
trgtidx_z = (target == 0)
# # Wird gleich benutzt um die Daten nach diesem target zu filtern

target_z_daten = data[trgtidx_z, :]

axs[0].plot(target_z_daten[:, 2], target_z_daten[:, 0],
            'o', label=target_names[0])

axs[0].legend()
axs[0].set_xlabel(feature_names[3])
axs[0].set_ylabel(feature_names[0])
axs[0].set_title(target_names[0])

plt.tight_layout()
plt.show()

Hier wurden die python Datentypen

  • list – z.B. datenpunkte = [1, 2, 3]
  • array – z.B. datenmatrix = np.array(datenpunkte)
  • dictionary – z.B. datadict = {'data': datenpunkte}

verwendet, die alle für verschiedene Zwecke gerne benutzt werden. Z.B.

  • Liste – als eine Sammlung von (möglicherweise total unterschiedlichen) Objekten, über die iteriert werden kann und die einfach zu erweitern ist
  • arrays – Matrix/Vektor von Daten eines Typs, mit denen gerechnet werden kann
  • dictionaries – ein Lookup table. Objekte können über einen Namen addressiert werden. Ich nehme sie gerne um Daten mit ihrem Namen zum Beispiel als json file zu speichern.

5.8.3 Pinguin Datensatz – 2D plots (P)

Erzeugen sie die Abbildung aller Merkmalpaare zum Beispiel über ein 4x4 Feld von subplots

fig, axs = plt.subplots(nrows=4, ncols=4, figsize=(10, 8))

erzeugen, in das sie mittels

axs[zeile, spalte].plot(xdaten, ydaten, 'o')

die plots fuer die einzelnen targets “eintragen” koennen. Bitte die Achsen beschriften (die legend ist nicht unbedingt notwendig).

5.8.4 Kovarianz (P)

Zentrieren Sie den Datensatz (zum Beispiel unter Verwendung der numpy.mean Funktion) und berechnen Sie die Kovarianzmatrix.

5.8.5 Hauptachsentransformation (P)

Berechnen sie Hauptachsen und stellen Sie die Daten in den Hauptachsenkoordinaten dar (wie in dieser Abbildung).

5.8.6 Kovarianzmatrix (T)

Zeigen sie, dass für zentrierte Datensätze \({\mathbf{X}}\in \mathbb R^{N\times n}\) gilt, dass \[\begin{equation*} \operatorname{Cov}(X) = \frac{1}{N-1}{\mathbf{X}}^T{\mathbf{X}}. \end{equation*}\]

5.8.7 Gesamtvarianz (T)

Zeigen sie, dass auch für \(n>2\) die Summe der Varianzen in orthogonalen Achsenrichtungen unabhängig von der Wahl des Koordinatensystems sind. (Vergleiche Kapitel 4.2 Koordinatenwechsel)

  1. allerdings mit 2 unvollständigen Datenpunkten, die ich entfernt habe für unseere Beispiele↩︎

  2. Im Originaldatensatz ist das Gewicht in Gramm angegeben, um die Daten innerhalb einer 10er Skala zu haben, habe ich das Gewicht auf in kg umgerechnet↩︎

  3. wir dürfen aber nicht vergessen, dass Daten typischerweise nur eine Stichprobe von Beobachtungen eines Phänomens sind. Die Unabhängigkeit in den features gilt also nur für die gesammelten Daten aber in der Regel nicht für das Phänomen. Für normalverteilte Prozesse liefern die daten-basiert ermittelten Hauptrichtungen jedoch auch die Hauptrichtungen des zugrundeliegenden Phänomens↩︎