2 Lineare Regression
Auch bekannt als
- lineare Ausgleichsrechnung oder
- Methode der kleinsten Quadrate.
Ein wesentlicher Aspekt von Data Science ist die Analyse oder das Verstehen von Daten. Allgemein gesagt, es wird versucht, aus den Daten heraus Aussagen über Trends oder Eigenschaften des Phänomens zu treffen, mit welchem die Daten im Zusammenhang stehen.
Wir kommen nochmal auf das Beispiel aus der Einführungswoche zurück, werfen eine bereits geschärften Blick darauf und gehen das mit verbesserten mathematischen Methoden an.
Gegeben seien die Fallzahlen aus der CoVID Pandemie 2020 für Bayern für den Oktober 2020.
| Tag | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|
| Fälle | 681 | 691 | 1154 | 1284 | 127 | 984 | 573 | 1078 | 1462 | 2239 |
| Tag | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
|---|---|---|---|---|---|---|---|---|---|---|
| Fälle | 2236 | 2119 | 1663 | 1413 | 2283 | 2717 | 3113 | 2972 | 3136 | 2615 |
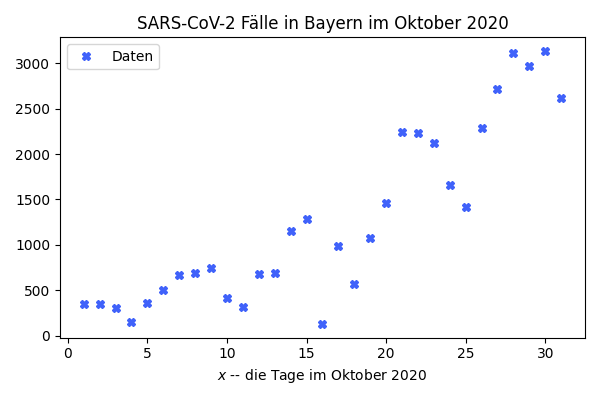
Fallzahlen von Sars-CoV-2 in Bayern im Oktober 2020
Wieder stellen wir uns die Frage ob wir in den Daten einen funktionalen Zusammenhang feststellen können. Also ob wir die Datenpaare
(Tag \(x\), Infektionen am Tag \(x\))
die wir als
(\(x_i\), \(y_i\))
über eine Funktion \(f\) und die Paare
(\(x\), \(f(x)\))
beschreiben (im Sinne von gut darstellen oder approximieren) können.
2.1 Rauschen und Fitting
Beim obigen Beispiel (und ganz generell bei Daten) ist davon auszugehen, dass die Daten verrauscht sind, also einem Trend folgen oder in einem funktionalen Zusammenhang stehen aber zufällige Abweichungen oder Fehler enthalten.
Unter diesem Gesichtspunkt ist eine Funktion, die
\(f(x_i)=y_i\)
erzwingt nicht zielführend. (Wir wollen Trends und größere Zusammenhänge erkennen und nicht kleine Fehler nachzeichnen.) Das zu strenge Anpassen an möglicherweise verrauschte Daten wird overfitting genannt.
Vielmehr werden wir nach einer Funktion \(f\) suchen, die die Daten näherungsweise nachstellt:
\(f(x_i)\approx y_i\)
Hierbei passen jetzt allerdings auch Funktionen, die vielleicht einfach zu handhaben sind aber die Daten kaum noch repräsentieren. Jan spricht von underfitting.
Eine gute Approximation besteht im Kompromiss von nah an den Daten aber mit wenig overfitting.
2.2 Ansätze für lineare Regression
Um eine solche Funktion \(f\) zu finden, trifft Jan als erstes ein paar Modellannahmen. Modellannahmen legen fest, wie das \(f\) im Allgemeinen aussehen soll und versuchen dabei
die Bestimmung von \(f\) zu ermöglichen
zu garantieren, dass \(f\) auch die gewollten Aussagen liefert
und sicherzustellen, dass \(f\) zum Problem passt.
Jan bemerke, dass die ersten beiden Annahmen im Spannungsverhältnis zur dritten stehen.
Lineare Regression besteht darin, dass die Funktion als Linearkombination
\[\begin{equation*} f_w(x) = \sum_{j=1}^n w_j b_j(x) \end{equation*}\]
von Basisfunktionen geschrieben wird und dann die Koeffizienten \(w_i\) so bestimmt werden, dass \(f\) die Daten bestmöglich annähert.
Jan bemerke, dass bestmöglich wieder overfitting bedeuten kann aber auch, bei schlechter Wahl der Basis, wenig aussagekräftig sein kann. Der gute Kompromiss liegt also jetzt in der Wahl der passenden Basisfunktionen und deren Anzahl. (Mehr Basisfunktionen bedeutet möglicherweise bessere Approximation aber auch die Gefahr von overfitting.)
Typische Wahlen für die Basis \(\{b_1, b_2, \dotsc, b_n\}\) sind
- Polynome: \(\{1, x, x^2, \dotsc, x^{n-1}\}\) – für \(n=2\) ist der Ansatz eine Gerade
- Trigonometrische Funktionen: \(\{1, \cos(x), \sin(x), \cos(2x), \sin(2x), \dotsc\}\)
- Splines – Polynome, die abschnittsweise definiert werden
- Wavelets – Verallgemeinerungen von trigonometrischen Funktionen
2.3 Fehlerfunktional und Minimierung
Wir setzen nun also an \[\begin{equation*} f_w(x) = \sum_{j=1}^nw_j b_j (x) \end{equation*}\] und wollen damit \(y_i \approx f_w(x_i)\) bestmöglich erreichen (indem wir die Koeffizienten \((w_1, \dotsc, w_n)\) optimal wählen. Bestmöglich und optimal spezifizieren wir über den Mittelwert der quadratischen Abweichungen in der Approximation über alle Datenpunkte \[\begin{equation*} \frac{1}{N}\sum_{i=1}^N (y_i - f_w(x_i))^2 \end{equation*}\]
Ein paar Bemerkungen
- jetzt müssen wir die \(w_i\)’s bestimmen so dass dieser Fehlerterm minimal wird
- das optimale \(w\) ist unabhängig von einer Skalierung des Fehlerterms
- des wegen schreiben wir gerne einfach \(\frac 12 \sum_{i=1}^N (y_i - f_w(x_i))^2\) als das Zielfunktional, das es zu minimieren gilt.
Wie finden wir jetzt die \(w_i\)’s? Zunächst gilt, dass \[\begin{equation*} f_w(x_i) = \sum_{i=j}^n w_j b_j(x_i) = \begin{bmatrix} b_1(x_i) & b_2(x_i) & \dots & b_n(x_i) \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix} \end{equation*}\]
und wenn wir alle \(f_w(x_i)\), \(i=1,\dotsc,N\) übereinander in einen Vektor schreiben, dass
\[\begin{equation*} f_w(\mathbf x) := \begin{bmatrix} f_w(x_1) \\ \vdots \\ f_w(x_N) \end{bmatrix} = \begin{bmatrix} b_1(x_1) & \dots & b_n(x_1) \\ \vdots & \ddots & \vdots \\ b_1(x_N) & \dots & b_n(x_N) \end{bmatrix} \begin{bmatrix} w_1 \\ \vdots \\ w_n \end{bmatrix} =: \Phi(\mathbf x) w \end{equation*}\]
Damit, mit \(\mathbf y\) als den Vektor aller \(y_i\)’s, und mit der Definition der Vektornorm, können wir unser Minimierungsproblem schreiben als \[\begin{equation*} \frac 12 \sum_{i=1}^N (y_i - f_w(x_i))^2 = \frac 12 \| \mathbf y - \Phi (\mathbf x) w\|^2 \to \min. \end{equation*}\]
Wir bemerken, dass
- das Fehlerfunktional immer größer und bestenfalls gleich 0 ist
- falls das lineare Gleichungssystem \(\Phi (\mathbf x)w = \mathbf y\) eine Lösung \(w\) hat, ist das auch eine Lösung unserer Minimierung
- im typischen Falle aber ist allerdings \(N\gg n\) und das System überbestimmt (\(n=N\) würde ein overfitting bedeuten…) sodass wir keine Lösung des linearen Gleichungssystems erwarten können.
- Das Minimierungsproblems selbst hat allerdings immer eine Lösung.
2.4 Berechnung der Bestlösung
Wir suchen also ein Minimum der Funktion (mit \(\Phi\), \(\mathbf x\), \(\mathbf y\) gegeben) \[\begin{equation*} \begin{split} w \mapsto \frac 12 \|\mathbf y - \Phi(\mathbf x)w \|^2 &= \frac 12 (\mathbf y - \Phi(\mathbf x)w)^T(\mathbf y - \Phi(\mathbf x)w) \\ &= \frac 12 [\mathbf y^T\mathbf y - \mathbf y^T \Phi(\mathbf x)w - w^T \Phi(\mathbf x)^T\mathbf y + w^T \Phi(\mathbf x)^T\Phi(\mathbf x)w] \\ &= \frac 12 [\mathbf y^T\mathbf y -2 w^T \Phi(\mathbf x)^T\mathbf y + w^T \Phi(\mathbf x)^T\Phi(\mathbf x)w] \end{split} \end{equation*}\] wobei wir die Definition der Norm \(\|v\|^2 = v^Tv\) und die Eigenschaft, dass für die skalare Größe \(w^T \Phi(\mathbf x)^T\mathbf y = [w^T \Phi(\mathbf x)^T\mathbf y]^T = \mathbf y^T \Phi(\mathbf x)w\) gilt, ausgenutzt haben.
Wären \(w\) und \(\mathbf y\) keine Vektoren sondern einfach reelle Zahlen, wäre das hier eine Parabelgleichung \(aw^2 + bw + c\) mit \(a>0\), die immer eine Minimalstelle hat.
Tatsächlich gilt hier alles ganz analog. Insbesondere ist \(\Phi(\mathbf x)^T\Phi(\mathbf x)\) in der Regel “größer 0” (was heißt das wohl bei quadratischen Matrizen?). Und mittels “Nullsetzen” der ersten Ableitung können wir das Minimum bestimmen. In diesem Fall ist die erste Ableitung (nach \(w\)) \[\begin{equation*} \nabla_w (\frac 12 \|\mathbf y - \Phi(\mathbf x) \|^2) = \Phi(\mathbf x)^T\Phi(\mathbf x)w - \Phi(\mathbf x)^T\mathbf y, \end{equation*}\] (den Gradienten \(\nabla_w\) als Ableitung von Funktionen mit mehreren Veränderlichen werden wir noch genauer behandeln) was uns als Lösung, die Lösung des linearen Gleichungssystems \[\begin{equation*} \Phi(\mathbf x)^T\Phi(\mathbf x)w = \Phi(\mathbf x)^T\mathbf y \end{equation*}\] definiert.
Letzte Frage: Wann hat dieses Gleichungssystems eine eindeutige Lösung? Mit \(N>n\) (also \(\Phi(\mathbf x)\) hat mehr Zeilen als Spalten) gelten die Äquivalenzen:
- \(\Phi(\mathbf x)^T\Phi(\mathbf x)w = \Phi(\mathbf x)^T\mathbf y\) hat eine eindeutige Lösung
- die Matrix \(\Phi(\mathbf x)^T\Phi(\mathbf x)\) ist regulär
- die Spalten von \(\Phi(\mathbf x)\) sind linear unabhängig
- die Vektoren \(b_i(\mathbf x)\) sind linear unabhängig.
Praktischerweise tritt genau diese Situation im Allgemeinen ein.
- \(N>n\) (mehr Datenpunkte als Parameter)
- \(b_i\)’s werden als linear unabhängig (im Sinne ihres Funktionenraums) gewählt, was die lineare unabhängigket der \(b_i(\mathbf x)\) impliziert.
2.5 Beispiel
Unsere Covid-Zahlen “mit einer Geraden angenähert”:
- \(f_w(x) = w_1 + w_2 x\) – das heißt \(n=2\) und Basisfunktionen \(b_1(x)\equiv 1\) und \(b_2(x) = x\)
- \(\mathbf x = (1,2,3, \dots, 31)\) – die Tage im Februar, das heißt \(N=31\)
- \(\mathbf y = (352, 347, \dots, 2615)\) – die Fallzahlen
Wir bekommen
\[\begin{equation*} \Phi(\mathbf x) = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \vdots & \vdots \\ 1 & 31 \end{bmatrix} \end{equation*}\] (die Spalten sind linear unabhängig) und müssen “nur” das 2x2 System \[ \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & 2 & 3 & \dots & 31 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \vdots \\ 1 & 31 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 & \dots & 1 \\ 1 & 2 & 3 & \dots & 31 \end{bmatrix} \begin{bmatrix} 352 \\ 347 \\ 308 \\ \vdots \\ 2615 \end{bmatrix} \] lösen um die Approximation \(f_w\) zu bestimmen.
Und noch als letzte Bemerkung. Egal wie die Basisfunktionen \(b_i\) gewählt werden, die Parameterabhängigkeit von \(w\) ist immer linear. Deswegen der Name lineare Ausgleichsrechnung.