8 Optimierung unter Nebenbedingungen

Oftmals werden an die gesuchte Lösung $x^* \in \mathbb R^{n}$ eines Optimierungsproblems a-priori bestimmte Anforderungen gestellt, wie:

$x_1 + x_2 \geq 0$ (die Lösung soll in einem bestimmten Abschnitt liegen)
$x_1^2 + x_2^2 - c^2 = 0$ (die ersten beiden Komponenten der Lösung sollen auf einer Kreisbahn liegen)

Allgemein lässt sich so ein Optimierungsproblem schreiben als

Definition 8.1 (Optimierungsproblem mit Nebenbedingungen) \[\begin{equation*} f(x) \to \min_{x\in \mathbb R^{n}}, \quad \text{s.t.} \quad g_i(x)\geq 0, \quad h_j(x) = 0, \end{equation*}\]

mit der Zielfunktion $f\colon \mathbb R^{n} \to \mathbb R^{}$
und zusätzlichen Nebenbedingungen (s.t. – subject to), die in
- Ungleichungsform über Funktionen $g_i\colon \mathbb R^{n} \to \mathbb R$, mit $i$ aus der Indexmenge $\mathcal I \subset \mathbb N$ oder
- Gleichungsform über Funktionen $h_j\colon \mathbb R^{n} \to \mathbb R$, mit $j$ aus der Indexmenge $\mathcal J \subset \mathbb N$ vorliegen können.

heißt restringiertes Optimierungsproblem oder Optimierungsproblem mit Nebenbedingungen

Liegen keine Gleichheits– oder keine Ungleichungsnebenbedingungen vor, setzen wir $\mathcal I = \emptyset$ oder $\mathcal J = \emptyset$.

Ein Optimierungsproblem ohne Nebenbedingungen heißt auch unrestringiertes Problem.

Jetzt stellt sich zur Frage ob ein $x^*$ optimal ist, noch die Frage, ob es auch zulässig (engl.: feasible) ist. Dazu lässt sich formal der Zulässigkeitsbereich (engl.: feasible set) definieren \[\begin{equation*} \Omega = \{x\in \mathbb R^{n} ~|~g_i(x)\geq 0, \quad h_j(x)=0, \quad i\in \mathcal I,\, j\in \mathcal J\} \end{equation*}\] und das Optimierungsproblem als \[\begin{equation*} f(x) \to \min_{x\in \Omega} \end{equation*}\] schreiben.

Die Definition 7.1 einer Minimalstelle gilt unmittelbar weiter, wenn nun auch der Zulässigkeitsbereich noch beachtet wird.

Die Unterscheidung von $D(f)$ und $\Omega$ in der Betrachtung des Optimierungsproblems und potentieller Minimalstellen hat diverse vor allem praktische Gründe:

der Definitionsbereich von $f$ ist eine vorgegebene Eigenschaft der Funktion während $\Omega$ vielleicht variiert werden soll
liegen nichttriviale Gleichheitsbedingungen vor, ist beispielsweise kein Punkt von $\Omega$ mehr ein innerer Punkt (im $\mathbb R^{n}$) und der Gradient von $f$ wäre erstmal nicht definiert
die Modellierung ist oftmals einfacher, wenn Nebenbedingungen einfach zum Problem hinzugefügt werden können
ebenso die Feststellung ob ein gegebener Punkt im Zulässigkeitsbereich liegt

Die Analysis restringierter Optimierungsprobleme und entsprechend die Umsetzung von Algorithmen zur Lösung wird durch die Nebenbedingungen ungleich schwieriger, da

in der Theorie nicht mehr einfach differenziert werden kann (insbesondere bei Gleichheitsbedingungen oder wenn der kritische Punkt am Rand der Ungleichungsbedingungen liegt) und
in der Umsetzung auf dem Computer darauf geachtet werden muss, dass der Zulässigkeitsbereich nicht verlassen wird.

8.1 Richtungen und Nebenbedingungen

Bei restringierten Optimierungsproblemen ist die Richtung in der analysiert wird entscheidend. Hierbei geht es darum ob in einer Richtung $v$

die Zielfunktion eventuell kleiner wird
der Zulässigkeitsbereich eventuell verlassen wird (bspw. charakterisiert durch $g(x) = 0$ oder $h(x)\geq0$)

Da es stets nur um die unmittelbare Umgebung eines Punktes geht, und wir aus der Diskussion der Ableitung (in 1D) wissen, dass eine differenzierbare Funktion lokal gut durch ihre Tangente angenähert werden kann¹⁰, können wir beide Betrachtungen in der lineaeren Approximation anstellen.

Wir schauen also ob für eine Richtung $v$ gilt, ob nicht

$f(x^*) > f(x^*+hv) \approx f(x^*) + \nabla f(x^*)^Tv$ bzw.
$0 \neq g(x^*+hv) \approx \nabla g(x^*)^Tv$ oder $0>h(x^*+hv) \approx \nabla h(x^*)^Tv$.

8.2 Restringierte Optimierungsprobleme und der Gradient

Zur Illustration und zur Einführung der Konzepte betrachten wir Probleme, die entweder nur Gleichungsnebenbedingungen oder nur Ungleichungsnebenbedingungen haben.

Wir beginnen mit Gleichungsnebenbedingungen und das auch nur im zweidimensionalen Fall: \[\begin{equation*} f(x,y) \to \min, \quad \text{s.t. }g(x,y)=c. \end{equation*}\] Aus der schematischen Darstellung in Abbildung 8.1 können wir ablesen, dass in einem potentiellen Extremum, die Gradienten von $f$ und $g$ in die gleiche Richtung zeigen, es also eine Skalar $\lambda$ geben muss, sodass in einem kritischen Punkt $(x^*, y^*)$ gilt, dass \[\begin{equation*} \nabla f(x^*, y^*) + \lambda \nabla g(x^*, y^*) =0 \end{equation*}\]

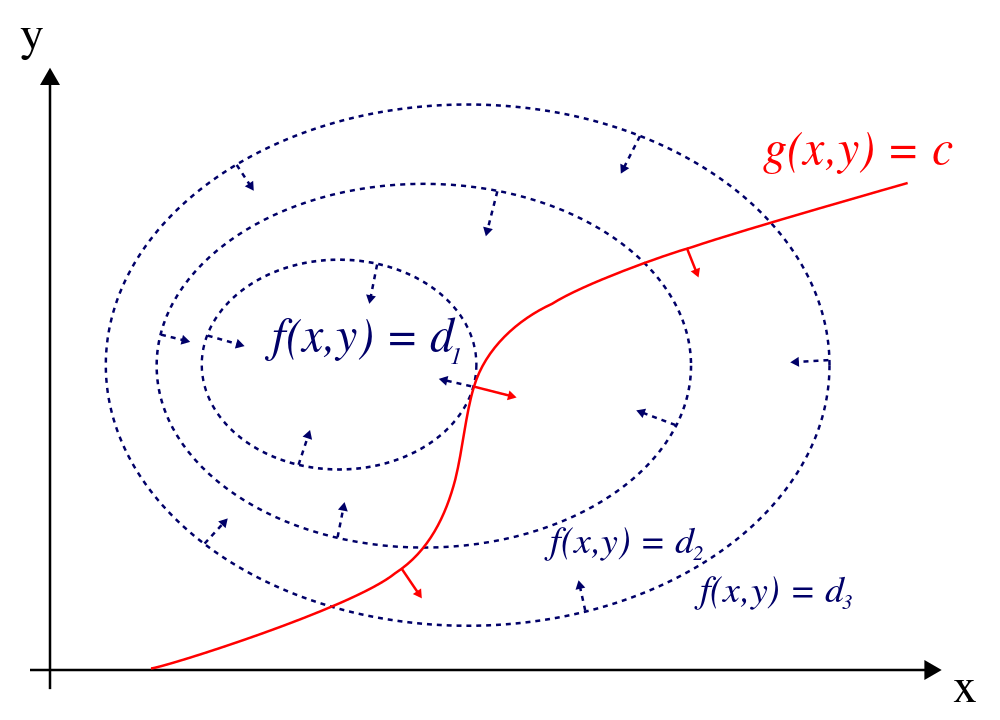
Figure 8.1: Schematische Darstellung eines Optimierungsproblems mit Gleichungsnebenbedingungen in 2D.

Wir könnten also versuchen, eine Lösung $(x,y,\lambda)$ für das Gleichungssystem \[\begin{equation} \begin{split} \nabla f(x, y) + \lambda \nabla g(x, y) &=0 \\ g(x,y) &= c \end{split} \tag{8.1} \end{equation}\] zu finden.

Dieses Gleichungssystem ist ein Spezialfall der Karush-Kuhn-Tucker Bedingungen, die ein notwendiges Kriterium für einen optimalen Punkt darstellen. Das involvierte $\lambda$ wird Lagrange Multiplikator genannt.

Dass an einem potentiellen Minimum gelten muss, dass $\nabla f(x^*) = -\lambda \nabla g(x^*)$ haben wir anhand einer Zeichnung im 2D Fall festgestellt.

Für $x\in \mathbb R^{n}$ und einer Gleichungsnebenbedingung $g$, ist die Argumentation wie folgt.

Lemma 8.1 Sei $x^*\in \mathbb R^{n}$ mit $g(x^*)=0$ so, dass $\nabla f$ und $\nabla g$ nicht parallel sind. Dann gilt für die Richtung \[\begin{equation*} v := -\biggl (I-\frac{1}{\|\nabla g(x^*)\|^2}\nabla g(x^*)g(x^*)^T \biggr )\nabla f(x^*) \end{equation*}\] dass $\nabla g(x^*)^Tv=0$ und $\nabla f(x^*)^Tv<0$ ist.

Lemma 8.1 sagt, dass es im skizzierten Fall also eine Richtung gibt, in der (in erster Ableitung) die Funktion $f$ minimiert werden kann ohne den Zulässigkeitsbereich zu verlassen.

8.3 Linear Quadratische Probleme

Ist die Zielfunktion als quadratische Funktion \[\begin{equation*} f(x) = x^T Q x + c^Tx \end{equation*}\] gegeben mit $Q\in \mathbb R^{n\times n}$ und $c\in \mathbb R^{n}$ und sind die Nebenbedingungen linear gegeben als \[\begin{equation*} Ax \geq b \end{equation*}\] mit $A\in \mathbb R^{m\times n}$, $b\in \mathbb R^{m}$ und mit $Ax \geq b$ bedeuten soll, dass alle Einträge des Vektors $Ax-b$ kleiner oder gleich $0$ sind, dann sprechen wir von einem (linearen) quadratischen Optimierungsproblem.

Hier müssen Gleichheitsbedingungen nicht explizit angeführt werden, da sie durch Ungleichungsbedingungen ausgedrückt werden können (vgl. $x=0$ gdw. $x\geq0$ und $-x\geq 0$).

Sind allerdings alle Bedingungen letztlich Gleichheitsbedingungen, liegt also das Problem als \[\begin{equation*} x^T Q x + c^Tx \to \min_{x\in \mathbb R^{n}} \quad \text{s.t. }Ax=b \end{equation*}\] vor, dann sind die notwendigen Optimalitätsbedingungen durch \[\begin{equation*} \begin{bmatrix} Q+Q^T & A^T \\ A & 0 \end{bmatrix} = \begin{bmatrix} -c \\ b \end{bmatrix}. \end{equation*}\]

Aus der Betrachtung dieser Optimalitätsbedingungen können wir folgern, dass, wenn $Q$ symmetrisch ist und positiv definit, sowie alle Zeilen von $A$ linear unabhängig sind, dass dann das Optimierungsproblem eine eindeutige Lösung hat, die durch die Optimalitätsbedingungen eindeutig charakterisiert ist.

8.4 Sequential Quadratic Programming

Aus der Beobachtung, dass wir LQP Probleme direkt mit $Q$ symmetrisch positiv definit direkt lösen können und dass wir für kleine Abweichungen $\xi$ von einem gebenen Punkt $x$ multivariable Funktionen über quadratische (für unser $f$) und lineare Approximationen (für unsere $g_i$) gut annähern können: \[\begin{equation*} f(x^*) = f(x+\xi) = f(x) + \nabla f(x)^T \xi + \xi^TH_f(x) \xi + \mathcal o(\| \xi \| ^2 ) \end{equation*}\] und \[\begin{equation*} g_i(x^*) = g_i(x+\xi) = g_i(\xi) + \nabla g_i(\xi)^T h + \mathcal o(\| \xi \|), \quad i \in \mathcal I, \end{equation*}\] ergibt sich das folgende iterative Verfahren genannt Sequential Linear Programming (SQP):

Beginnend von einem Näherungswert $x^k$

Berechne $d^k$ aus der Minimierung von¹¹ \[\begin{align*} \tilde f(x^k+d):= \nabla f(x^k)^T d + d^TH_f(x^k) d \to \min_{d\in \mathbb R^{n}}, \\\quad \text{unter der Nebenbedingung} \\ \tilde g_i(x^k+d):=g(x^k)+\nabla g_i(x^k)d = 0 \quad i \in \mathcal I \end{align*}\]
ein Update $x^{k+1}=x^k+d^k$.

Es ist also in jeder Iteration ein linear quadratisches Optimierungsproblem \[\begin{equation*} x^T Q_k x + c_k^Tx \to \min_{x\in \mathbb R^{n}} \quad \text{s.t. }A_kx=b_k \end{equation*}\] zu lösen, wobei (in der obigen Notation mit $Q$, $c$, $A$ und $b$) gilt dass \[\begin{equation*} Q_k=H_f(x^k), \quad c_k=\nabla f(x_k) \end{equation*}\] und \[\begin{equation*} A_k = \begin{bmatrix} \nabla g_i(x_k)^T \end{bmatrix}_{i \in \mathcal I} \in \mathbb R^{|\mathcal I| \times n}, \quad b_k = - \begin{bmatrix} g_i(x_k) \end{bmatrix}_{i \in \mathcal I}\in \mathbb R^{|\mathcal I|}. \end{equation*}\]

Ist die Funktion $f$ konvex und zweimal stetig differenzierbar (in einer Umgebung von $x_k$), dann ist die Hesse-matrix $H_f(x_k)$ positiv definit und das LQP hat eine eindeutige Lösung $x_{k+1}$.

8.5 Aufgaben

8.5.1 KKT für LQP (T)

Verifizieren Sie, dass die notwendigen Optimalitätsbedingungen für das LQP Problem mit Gleichungsnebenbedingungen (mit $m=1$) genau der Optimalitäsbedingung aus Gleichung (8.1) entspricht. Hinweis: Mit der Definition der totalen Ableitung und der Relation zum Gradienten für reellwertige multivariable Funktionen (vgl. die Vorlesung Mathe für DS2 vom 6. Juli) ist eine Darstellung der Gradienten $\nabla f(x)$ und $\nabla g(x)$ direkt herleitbar.

8.5.2 Nicht parallele Gradienten (T)

Verifizieren sie die Aussage aus Lemma 8.1.

8.5.3 Hauptkomponente aus SQP (T+P)

Skizzieren sie das Optimierungsproblems, das die letzte Hauptkomponentenrichtung definiert (also die Richtung mit minimaler Varianz) eines zentrierten Datensatzes definiert (analog dazu, wie in Abschnitt 4.3 eingeführt). Hinweis: Alles wird vielleicht etwas einfacher, wenn sie die Nebenbedingung $\|x\|=1$ durch $\|x\|^2 = 1$ bzw. $x^Tx = 1 $ ersetzen. (T)

Skizzieren einen SQP-Schritt zur Lösung dieses Problems. (T)

Implementieren sie die SQP Iteration zur Berechnung der letzten Hauptkomponentenrichtung für die Pinguin Daten. Berechnen Sie die Abweichung zur exakten (mit der SVD berechneten) Lösung und geben sie ihn in jedem Schritt beispielsweise den Winkel zwischen dem Iteranten und der exakten Loesung berechnen. Hinweis: Nur die Norm der Differenz könnte irritieren, weil das Vorzeichen der Richtungen nicht festgelegt ist.

import json
import numpy as np

with open('penguin-data.json', 'r') as f:
    datadict = json.load(f)

data = np.array(datadict['data'])

# center the data
X = data - data.mean(axis=0)
XtX = X.T @ X  # for later use

U, S, Vh = np.linalg.svd(X)

pcfour = Vh[-1:, :].T  # die "letzte" Hauptrichtung
nrmpcf = np.linalg.norm(pcfour)  # brauchen wir um den Winkel zu berechnen

xk = np.zeros((4, 1))  # Startvektor
xk[0] = 1
arccosalpha = xk.T @ pcfour / (np.linalg.norm(xk)*nrmpcf)
print(f'Iteration: {0} -- `arccos(sol, xk)` {arccosalpha}')


def solve_sadpoint_sys_x(Q=None, A=None, fone=None, ftwo=None):
    ''' Loesung des Sattelpunktprobles

    | Q  A.T | . | x |    | f1 |
    | A   0  |   | l |  = | f2 |

    Notes:
    -----

    Es wird nur `x` zurueckgegeben

    '''
    m = A.shape[0]
    lineone = [Q, A.T]
    linetwo = [A, np.zeros((m, m))]
    sdptmat = np.vstack([np.hstack(lineone),
                         np.hstack(linetwo)])
    rhs = np.vstack([fone, ftwo])
    xl = np.linalg.solve(sdptmat, rhs)
    return xl[:-m]  # return only the `x-part`


for kkk in range(1, 11):
    # ...
    # die SQP Iteration
    # ...
    xk = xk + solve_sadpoint_sys_x()

    arccosalpha = xk.T @ pcfour / (np.linalg.norm(xk)*nrmpcf)
    print(f'Iteration: {kkk} -- `arccos(sol, xk)` {arccosalpha}')

gut im Sinne von der Fehler $f(x+h)-f(x)-f'(x)h$ geht schneller zur $0$ als $h$↩︎
Die korrekte quadratische Approximation von $f$ würde noch den Term $f(x^k)$ enthalten. Dieser kann aber einfach weggelassen werden bei der Suche der Minimalstelle.↩︎