1 Was ist Data Science?

Data Science umfasst unter anderem folgende Aufgaben:

Strukturieren/Aufbereiten (Umgehen mit falschen, korrumpierten, fehlenden, unformatierten Daten)
Data Exploration (Daten “verstehen”)
Data Analysis (quantitative Analysen, Hypothesen aufstellen)
Data Visualization (Hypothesen graphisch kommunizieren)
Modelle erzeugen/validieren (Regeln/Muster erkennen, Vorhersagen treffen) – das ist Machine Learning aber es gibt auch viele andere Ansätze.
Daten Reduktion

1.1 Wie passiert die Datenanalyse?

Mit mathematischen Methoden aus den Bereichen der

linearen Algebra (z.B. Matrizen, Basen, lineare Gleichungssysteme)
Statistik (z.B. Mittelwerte, Korrelationen, Verteilungen)
Analysis (Grenzwerte, Abschätzungen)
…

Dabei hilft Software, z.B.,

Excel
Python
Matlab
R

bei der Berechnung, Automatisierung, Visualisierung.

Python ist ein de-facto Standard in Data Science und Machine Learning.

1.2 Was sind Daten?

Wie sehen Daten aus?

Numerisch reell, z.B. Temperatur
Numerisch diskret, z.B. Anzahl
Ordinal: Element einer festen Menge mit expliziter Ordnung, z.B. {neuwertig, mit Gebrauchsspuren, defekt}
Binär: Eine von zwei Möglichkeiten, z.B. Wahr/Falsch oder aktiv/inaktiv
Kategoriell: Element einer festen Menge ohne klare Ordnung, z.B. {Säugetier, Vogel, Fisch}
sonstige strukturierte Daten, z.B. geographische Daten, Graphen
reiner Text, z.B. Freitext in Restaurantbewertung

Außerdem können wir noch allgemeine Eigenschaften (Qualitätsmerkmale) von Daten unterscheiden

strukturiert
lückenhaft
fehlerbehaftet (verrauscht)
interpretierbar
geordnet (oder nicht zu ordnen)

1.3 Beispiele

1.3.1 Tabellendaten – Mietpreise

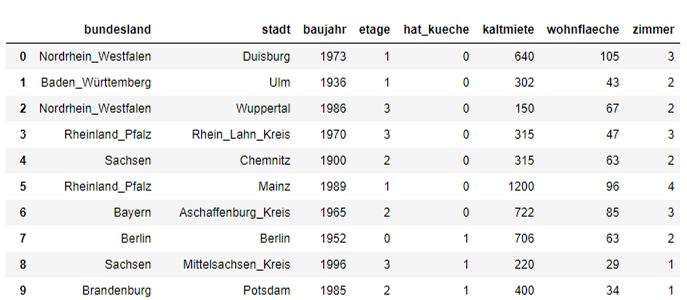
Abbildung: Tabelle von Wohnungsangeboten

Hier wären die Aufgaben von Data Science:

Daten “verstehen”, Zusammenhänge zwischen Variablen aufdecken,
visualisieren.
Gegebenenfalls fehlende Einträge bei (z.B.) kaltmiete vorhersagen

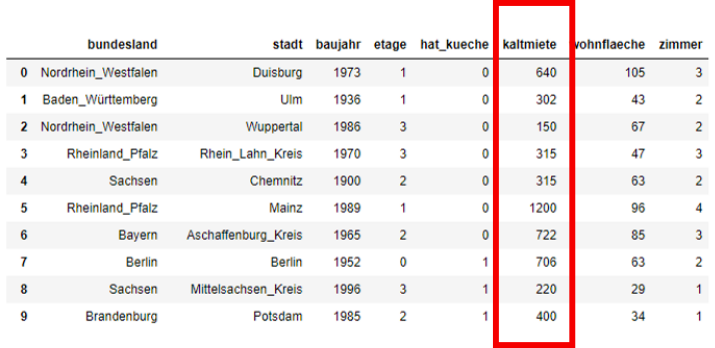
Abbildung: Eine Spalte der Tabelle

Datenexploration und -analyse für einzelne Variablen 1/3 Wir betrachten eine numerische Variable in einem rechteckigen Datensatz, also eine Spalte (z.B. kaltmiete). Wir bezeichnen den $i$ -ten Eintrag in dieser Spalte mit $x_i$ , wobei $i=1,\ldots,N$ ( $N$ Anzahl der Zeilen).

Folgende Schätzer/Metriken können dabei helfen, diese Spalte besser zu verstehen:

Mittelwert $\overline x= \frac1 N\sum_{i=1}^N x_i$
gewichteter Mittelwert $\overline x_w = \frac{\sum_{i=1}^N w_i x_i}{\sum_{j=1}^N w_j}$ , wobei $w_i$ das Gewicht des $i$ -ten Eintrages ist (z.B. eine andere Variable).
Varianz: $s_x^2 = \frac{1}{N-1} \sum_{i=1}^N (x_i-\overline x)^2$
Standardabweichung $s = \sqrt{s_x^2}$ .
Median = $\frac{315 + 400}{2} = 357.5$ .

Datenexploration und -analyse für mehrere Variablen Wir betrachten zwei Spalten $x = (x_1,\ldots,x_N)$ und $y = (y_1,\ldots, y_N)$ .

Das Verteilung von zwei Variablen läßt sich im sogenannte Scatter Plot visualisieren.

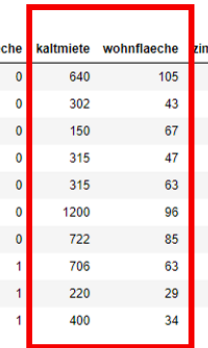
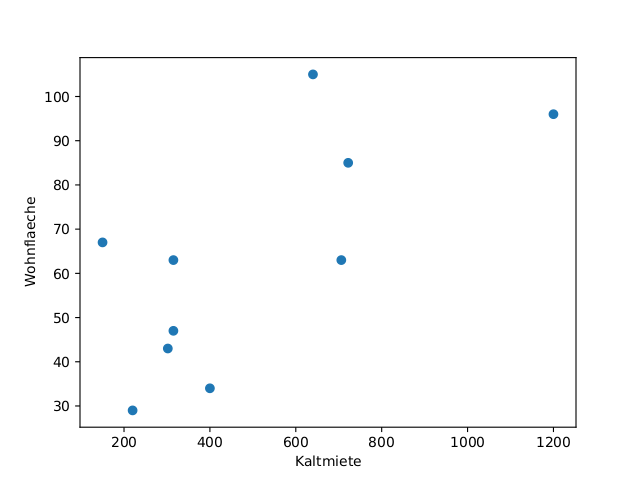
Kaltmiete versus Wohnfläche als Scatterplot

Datenexploration und -analyse für mehrere Variablen Wir betrachten zwei Spalten $x = (x_1,\ldots,x_N)$ und $y = (y_1,\ldots, y_N)$ .

Kovarianz $s_{xy} = \frac{1}{N-1}\sum_{i=1}^N (x_i - \overline x)(y_i - \overline y)$
Korrelation $\rho_{xy} = \frac{s_{xy}}{s_x\cdot s_y} \in [-1,1]$ .
$\rho \approx 1$ : Starke positive Korrelation, wenn $x$ groß ist, ist $y$ auch groß.
$\rho \approx -1$ : Starke negative Korrelation, wenn $x$ groß ist, ist $y$ klein
$\rho \approx 0$ : Wenig/keine Korrelation.

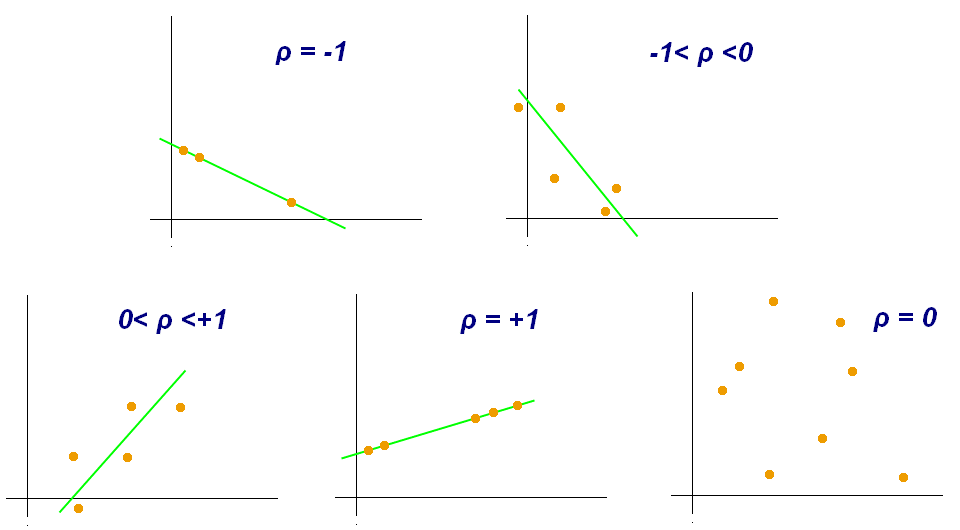
Von Kiatdd - Eigenes Werk, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=37108966

1.3.2 COVID-19 Daten

Vergleiche die Einführung in Mathematik für Data Science 1 vom letzten Semester.

1.3.3 Netflix Prize

Hierbei geht es darum, ob aus bekannten Bewertungen von vielen verschiedenen Benutzern für viele verschiedene Filme abgeleitet werden kann, ob ein bestimmter Nutzer einen bestimmten Film mag (also positiv bewerten würde).

Vergleiche auch Wikipedia:Netflix_Prize

Das (Trainings-)Daten bestehen über 480189 Benutzer, die für 17770 Filme insgesamt 100480507 Bewertungen als ganze Zahlen zwischen 1 und 5 verteilten.

Ziel der Datenanalyse war es, für 2817131 “Paare” von Benutzern und Filmen, die Bewertung vorauszusagen. Neben der schieren Masse an Daten kamen noch Einschränkungen hinzu, die ein Mindestmaß an Qualität der Vorhersage sicherstellen sollten.

Das Problem ließe sich wie folgt darstellen.

Benutzer \ Film	`F1`	`F2`	`...`	`Fn`	`...`
`B1`	–	3	`...`	5	`...`
`B2`	3	4	`...`	2	`...`
`B3`	1	2	`...`	?	`...`
`...`	3	4	`...`	–	`...`

Gegeben viele (aber bei weitem nicht alle) Einträge in einer riesigen Tabelle. Können wir aus den Zusammenhängen bestimmte fehlende Einträge (z.B. wie findet Nutzer B3 den Film Fn) herleiten?

Die besten Lösungen für dieses Problem basieren durchweg auf Machine Learning Ansätzen.

1.4 Python

Die Programmiersprache python wird uns durchs Semester begleiten. Einfach weil sie so wichtig ist für Data Science aber auch weil sie (meiner Meinung nach) einfach zu erlernen und zu benutzen ist.

1.5 Aufgaben

1.5.1 Python

Bringen sie ihr python zum Laufen, installieren sie numpy, scipy und matplotlib und führen sie das folgende script aus.

import numpy as np
import matplotlib.pyplot as plt

N = 20
xmax = 2
xmin = 0

xdata = np.linspace(xmin, xmax, N)
ydata = np.exp(xdata)

plt.figure(1)
plt.plot(xdata, ydata, '.')

plt.figure(2)
plt.semilogy(xdata, ydata, '.')
plt.show()

1.5.2 Einheitsmatrix

Schreiben sie ein script, dass die 5x5 Einheitsmatrix auf 3 verschiedene Arten erzeugt. (Eine Art könnte die eingebaute numpy Funktion eye sein).

import numpy as np

idfive = np.eye(5)
print(idfive)

Hinweis: schauen sie sich mal an wie numpy’s arrays funktionieren.

1.5.3 Matrizen Multiplikation und Potenz

Schreiben sie ein script, das die Übungsaufgabe aus der Vorlesung (potenzieren der Matrizen $M_i$ , $i=1,2,3,4$ ) löst. Zum Beispiel mit

import numpy as np
mone = np.array([[0.9, 0.9], [0.9, 0.9]])

mone_ptwo = mone @ mone
print(mone_ptwo)

mone_pfour = mone_ptwo @ mone_ptwo
print(mone_pfour)

Oder so:

import numpy as np
mone = np.array([[0.9, 0.9], [0.9, 0.9]])
mone_p = np.eye(2)

for k in range(16):
    mone_p = mone_p @ mone
    if k == 1 or k == 3 or k == 15:
        print('k=', k+1)
        print(mone_p)

Achtung:

bei Matrizen kann auch * benutzt werden – das ist aber nicht die richtige Matrizenmultiplikation (sondern die Multiplikation eintragsweise)
Moegliche Realisierung der Matrizenmultiplikation
- np.dot(A, B) – die klassische Methode
- A.dot(B) – das selbe (manchmal besser, wenn A etwas allgemeiner ist (zum Beispiel eine scipy.sparse matrix)
- A @ B – convenience Notation