FEniCS Burgers POD DMD

Table of Contents
Burgers equation
For a given viscosity parameter $\nu$ and for time $t>0$, we consider the 2D Burgers equation on the unit square
$$ \frac {\partial}{\partial t}u + (u\nabla)u - \nu \Delta u = 0 $$with zero Neumann boundary conditions and initial condition
$$ u\bigr| _ {t=0}(x _ 1, x _ 2) = \begin{bmatrix} 1 \\\\ 1 \end{bmatrix} e ^ {-(4x _ 1^2 + 2x _ 2^2)} $$and its numerical approximation using
- Finite Elements in space and Runge-Kutta in time,
- a POD reduction of the FEM model, and
- a DMD reduced order model.
burgers.py for the presented code (and more) in one file.
0. The Setup
We start with importing the necessary modules and defining the parameters.
import dolfin
import scipy.linalg as spla
import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import solve_ivp
from spacetime_galerkin_pod.ldfnp_ext_cholmod import SparseFactorMassmat
dolfin.parameters['linear_algebra_backend'] = 'Eigen'
nu = 1e-4 # the viscosity
N = 80
poddim = 30
t0, tE, Nts = 0., .8, 101 # the time grid for the snapshots
timegrid = np.linspace(t0, tE, Nts)
Here, dolfin is the python interface to FEniCS
and the other modules are standard in python, I would say. The module
ldfnp_ext_cholmod is a little wrapper for the sparsity optimizing Cholesky
decomposition of sksparse.
It is available on github
and falls back to numpy routines, in the case that sksparse is not
available.
1. The FEM Discretization
The spatial discretization in FEniCS
First, the mesh is defined – here a uniform triangulation of the unit square
controlled by the parameter N. For the value N=80 and for globally smooth
and piecewise quadratic ansatz functions, the resulting dimension of the system
is 51842.
# The mesh
pone = dolfin.Point(-1, -1)
ptwo = dolfin.Point(1, 1)
mesh = dolfin.RectangleMesh(pone, ptwo, N, N)
V = dolfin.VectorFunctionSpace(mesh, 'CG', 2)
# ## The FENICS FEM Discretization
v = dolfin.TestFunction(V)
u = dolfin.TrialFunction(V)
Next, the discrete linear operators are defined and exported as a SciPy sparse
matrix. Also, we factorize the mass matrix mmat for later use and define the
norm that is weighted with the mass matrix as this is the discrete $L^2$ norm.
# ## the mass matrix
mform = dolfin.inner(v, u)*dolfin.dx
massm = dolfin.assemble(mform)
mmat = dolfin.as_backend_type(massm).sparray()
mmat.eliminate_zeros()
# factorize it for later
mfac = SparseFactorMassmat(mmat)
# norm induced by the mass matrix == discrete L2-norm
def mnorm(uvec):
return np.sqrt(np.inner(uvec, mmat.dot(uvec)))
# ## the stiffness matrix
# as a form in FEniCS
aform = nu*dolfin.inner(dolfin.grad(v), dolfin.grad(u))*dolfin.dx
aassm = dolfin.assemble(aform)
# as a sparse matrix
amat = dolfin.as_backend_type(aassm).sparray()
amat.eliminate_zeros()
Then we define the convective term as function of the velocity u both in terms
of an FE-function and as a function of the associated coefficient vector.
# ## the convective term
# as a function in FEniCS
def burgers_nonl_func(ufun):
cform = dolfin.inner(dolfin.grad(ufun)*ufun, v)*dolfin.dx
cass = dolfin.assemble(cform)
return cass
# as a vector to form map
def burgers_nonl_vec(uvec):
ufun = dolfin.Function(V)
ufun.vector().set_local(uvec)
bnlform = burgers_nonl_func(ufun)
bnlvec = bnlform.get_local()
return bnlvec
The Runge-Kutta Time Integration
To apply standard time integration schemes (here, RK23 turned out to be most
efficient), we define the right hand side $f_h$ of the spatially discretized problem
In this case the right hand side is an application of the discrete diffusion
and convection operator and the inverse of the mass matrix that, simply
speaking, maps a (discrete) form onto a discrete function. Note that there is no
explicit time dependency in the Burgers equation, but the SciPy’s solve_ivp
requires this parameter. Also, we define the initial value here. The time grid
is used to store the solution for the snapshots needed later, but the time
integrator uses his internal time grid.
inivstrg = 'exp(-3.*(x[0]*x[0]+x[1]*x[1]))'
inivexpr = dolfin.Expression((inivstrg, inivstrg), degree=2)
inivfunc = dolfin.interpolate(inivexpr, V)
inivvec = inivfunc.vector().get_local()
burgsol = solve_ivp(brhs, (t0, tE), inivvec, t_eval=timegrid, method='RK23')
fullsol = burgsol.y
Here is the result. Note the sharp front that develops towards the end of the time integration.
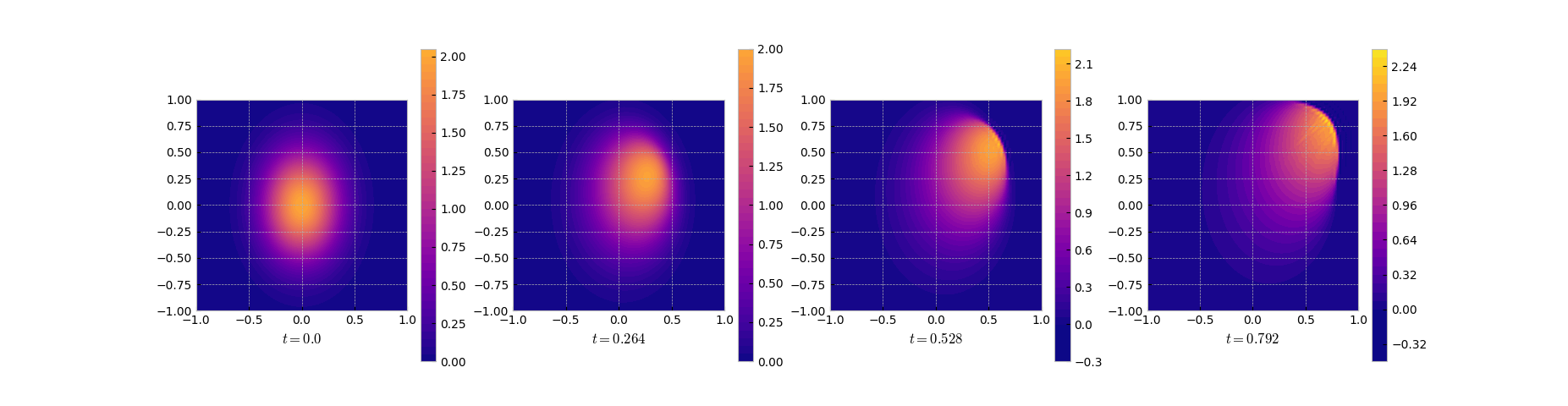
Solution snapshots of the full FEM model
2. POD Reduced Model
If one has snapshots of the solution $v _ h$ at some time instances $t _ i$ one may well think that the span of the matrix of snapshots
$$ X = \begin{bmatrix} v _ h(t_0) & v _ h(t_1) & \dotsm & v _ h(t_k) \end{bmatrix} $$is a good candidate for a space in which the solution evolves in. One may even go further and look for a low-dimensional basis of this space. The span of a matrix is best approximated by its dominant singular vectors. And this is the idea of Proper Orthogonal Decomposition (POD) – use the leading singular vectors as a basis for the solution space.
We use the Nts=101 snapshots of the FEM solutions to setup the matrix of
measurements $X$ and to compute the POD modes as $M^{-1/2}v _ k$, where $v _ k$
is the $k$-th leading left singular vector of $M^{1/2}X$. This procedure gives a
low-dimensional orthogonal (in the discrete $L^2$ inner product) basis that
optimally parametrizes the subspace of $L^2$ that is spanned by the solution
snapshots1. In this example, we use the poddim=30 leading singular vectors
to define the reduced model.
snapshotmat = mfac.Ft.dot(burgsol.y)
podmodes, svals, _ = spla.svd(snapshotmat, full_matrices=False)
selected_podmodes = podmodes[:, :poddim]
podvecs = mfac.solve_Ft(selected_podmodes)
In this implementation we use a sparse factor of the mass matrix instead of the square root. The singular values (in particular those that correspond to the discarded directions) give an indication of how good the approximation is.

The singular values of the snapshot matrix
Here, the decay is comparatively slow, so that a one should not expect a good low dimensional approximation by POD.
For the simulation, the state is parametrized by $u_h (t) \approx V \tilde
u_h(t)$ where $V$ is the matrix of the POD modes (in the code $V$ denoted by
podvecs), which gives a system in $\tilde u _ h$ with 30 degrees of freedom
(as opposed to the 51842 of the full order model).
redamat = podvecs.T.dot(amat.dot(podvecs)) # the projected stiffness
def redbrhs(time, redvec):
inflatedv = podvecs.dot(redvec)
redconv = podvecs.T.dot(burgers_nonl_vec(inflatedv))
return -redamat.dot(redvec) - redconv.flatten()
Here we define the projected stiffness matrix and the reduced nonlinearity through
- inflating the reduced state to full dimension
- applying the nonlinearity
- projecting down the result.
This means that our model is not completely independent of the full dimension. For this problem there are hyperreduction techniques like DEIM.
Thus, the right hand side is readily defined the more that the projected mass matrix is the identity. Why?
Finally, the initial value is projected into the reduced coordinates and the reduced system is integrated in time.
redburgsol = solve_ivp(redbrhs, (t0, tE), prjinivvec,
t_eval=timegrid, method='RK23')
podredsol = redburgsol.y
In the solution we see that the reduced order model gives a decent approximation in the smooth regime in the beginning and even well approaches the front as can be seen in the error (log) plot.

Snapshots of the solution of the reduced system

Snapshots of the log of the error between the full and the POD solution
3. DMD Reduced Model
POD is partially data driven – it uses data to create a basis but still uses (a projection of) the model. If only snapshots but no model is given, one may use the method of Dynamic Mode Decomposition2 (DMD) that tries to identify a matrix $A$ that evolves the state like
$$ A v _ h (t_i) = v _ h (t _ {i+1}) $$In practice, one uses a set of snapshots and the two measurement matrices
$$ X = \begin{bmatrix} v _ h(t_0) & v _ h(t_1) & \dotsm & v _ h(t _ {k-1}) \end{bmatrix} $$and
$$ X' = \begin{bmatrix} v _ h(t_1) & v _ h(t_2) & \dotsm & v _ h(t _ {k}) \end{bmatrix}. $$Note that $X'$ is basically $X$ shifted by one time step.
Then the DMD matrix can be found by solving the linear regression problem
$$ \min _ P \| X' - PX \| _ F. $$For the reduced DMD model we use the same snapshot matrix as for the POD. The regression problem is solved via SVD to compute the needed pseudo inverse since this naturally allows for a rank reduction and a factored representation of the DMD matrix.
# ### dmd using truncated svd inverse
fburgsol = burgsol.y
Xmat = fburgsol[:, :-1]
Xdsh = fburgsol[:, 1:]
ux, sx, vxh = spla.svd(Xmat, full_matrices=False)
uxr, sxr, vxhr = ux[:, :poddim], sx[:poddim], vxh[:poddim, :]
# compute the dmd matrix in factored form: `dmda = dmdaone * dmdatwo`
dmdaone = Xdsh.dot(vxhr.T)
dmdatwo = np.linalg.solve(np.diag(sxr), uxr.T)
Once the DMD matrix $A$ is determined, the simulation of the DMD reduced model is only a repeated multiplication by $A$.
# simulation of the dmd reduced model
dmdxo = inivvec
dmdsol = [dmdxo]
for k in np.arange(Nts):
dmdsol.append(dmdaone.dot(dmdatwo.dot(dmdsol[-1])))
dmdsol = np.array(dmdsol).T
As can be seen from the results and the error plots, DMD does a good job in the initial phase but fails in the region with the sharp front.
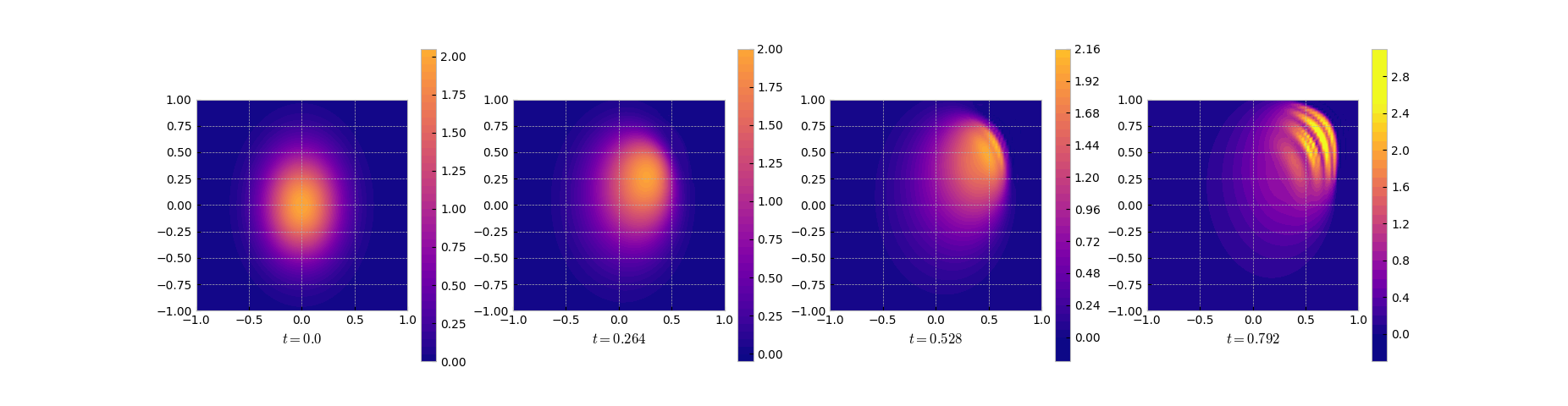
Snapshots of the DMD solution
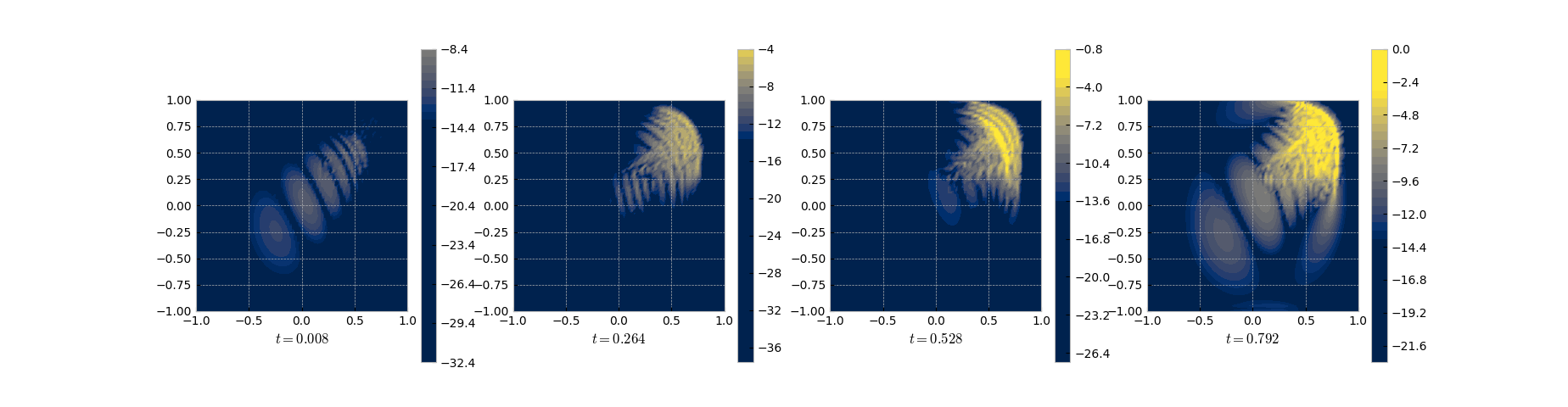
Error (log) plot with respect to the full FEM solution
4. Testing the Models for Different Initial Value
In what was presented above, the reduced models were used to reproduce the states that they were trained on. We now check the given reduced order models but on an alternative initial value, namely
$$ u\bigr| _ {t=0}(x _ 1, x _ 2) = \begin{bmatrix} 1 \\\\ 1 \end{bmatrix} e ^ {-(2x _ 1^2 + 4x _ 2^2)} $$see the following two plots of the full order model for both initial values.

Solution snapshots of the full FEM model
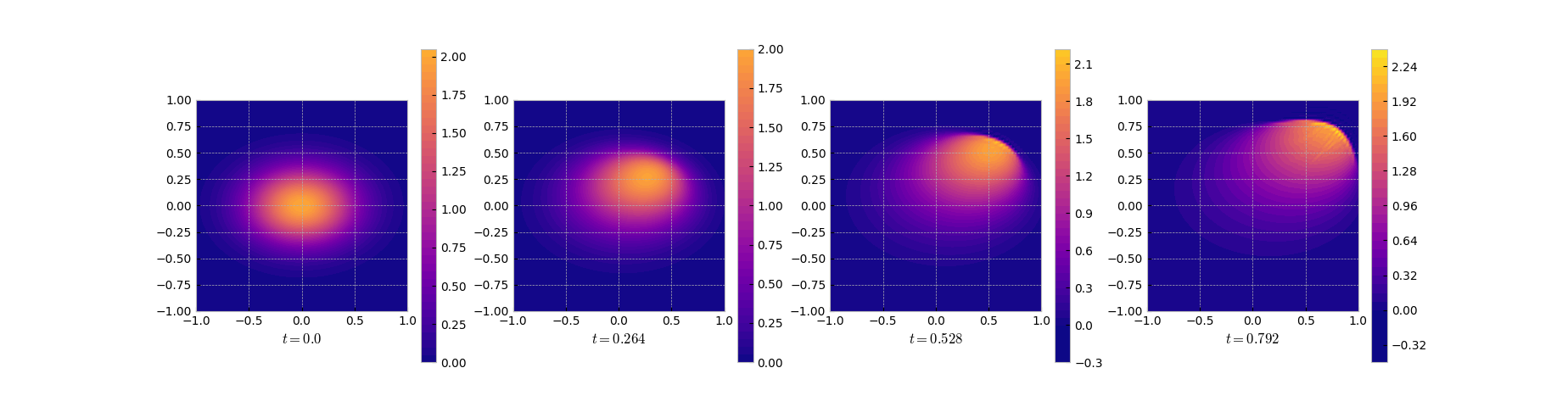
Solution snapshots of the full FEM model with the alternative initial value
Then we use the reduced order models to compute predictions for the trajectory starting in this alternative initial value.

Snapshots of the solution of the POD reduced system starting in the alternative initial value.
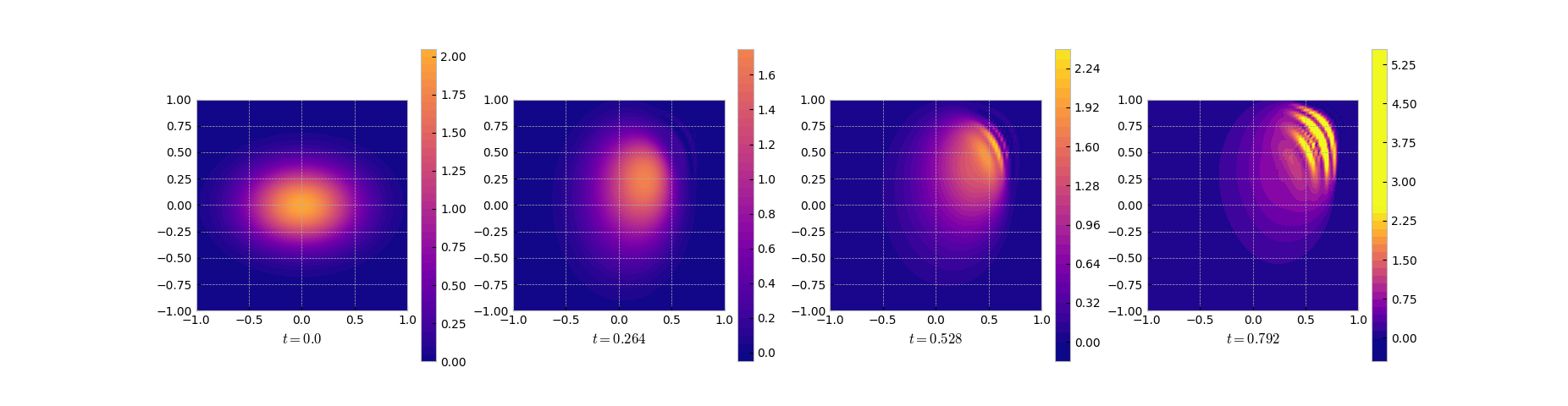
Snapshots of the DMD solution starting in the alternative initial value.
Both methods completely fail to produce the other trajectory. For the POD reduced model already the starting point is extremely bad approximated. Interestingly, although the DMD solution starts in the right point, it seems to exactly reproduce the solution that it was trained on up to some additional oscillations.
5. Remarks
It is commonly accepted that POD does not work well for transport dominated
problems – like the current case with the low viscosity parameter nu=1e-4.
So, I think that the results for POD are quite good noting that the reduced
order model has 30 degrees of freedom whereas the full model has 51842.
In my tests, increasing the number of basis functions as well as considering a
larger nu led to better POD approximations.
The DMD approach shows a similar performance. If compared to POD, the qualitative approximation looks less good but the numbers are slightly better. All in all, the DMD approximation seems less reliable as for other parameter choices, the performance rather deteriorated than improved.
How challenging the problem of 2D Burgers with a low viscosity is, can be seen from the failure of both methods to produce useable approximations to trajectories that start in different initial values.
-
See, e.g., Lemma 2.5 of Baumann, Benner, and Heiland (2018): Space-Time Galerkin POD with Application in Optimal Control of Semi-linear Parabolic Partial Differential Equations. arXiv:1611.04050 ↩︎
-
See, e.g., Tu, Rowley, Luchtenburg, Brunton, Kutz (2013): On Dynamic Mode Decomposition: Theory and Applications arXiv:1312.0041 ↩︎