Polytopic Autoencoders with Smooth Clustering for Reduced-order Modelling of Flows

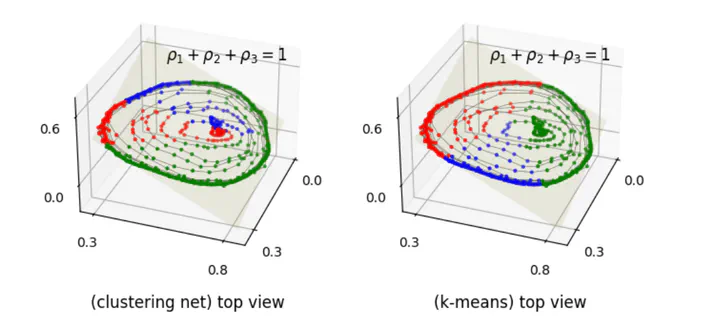
With the advancement of neural networks, there has been a notable increase, both in terms of quantity and variety, in research publications concerning the application of autoencoders to reduced-order models. We propose a polytopic autoencoder architecture that includes a lightweight nonlinear encoder, a convex combination decoder, and a smooth clustering network. Supported by several proofs, the model architecture ensures that all reconstructed states lie within a polytope, accompanied by a metric indicating the quality of the constructed polytopes, referred to as polytope error. Additionally, it offers a minimal number of convex coordinates for polytopic linear-parameter varying systems while achieving acceptable reconstruction errors compared to proper orthogonal decomposition (POD). To validate our proposed model, we conduct simulations involving two flow scenarios with the incompressible Navier-Stokes equation. Numerical results demonstrate the guaranteed properties of the model, low reconstruction errors compared to POD, and the improvement in error using a clustering network.

Manuscript